Microscopic Characterization of 2D Materials by Spectroscopic Imaging Ellipsometry
Imaging Ellipsometry
Imaging ellipsometry, combines the power of ellipsometry with optical microscopy. It achieves the highest lateral resolution in the field of ellipsometry and offers a very sensitive imaging technology for thin films. Typical samples range from tiny samples like flakes of 2D materials to inhomogeneous surfaces like some CWD samples of 2D materials or terraces at Epitaxial Graphene surfaces.
The ep4 is the latest microscopic imaging spectroscopic ellipsometer with unique measurement cap- abilities. It can provide real-time ellipsometric enhanced contrast images, and maps of the ellipso- metric angles Psi and Delta. These data can be transferred into Thickness and the complex refractive indices by computerized optical modeling.
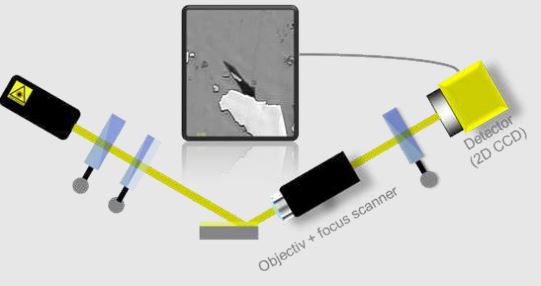
Setup of an imaging ellipsometer including objective and 2D CCD.

Imaging spectroscopic ellipsometer nanofilm_ep4.
Regions of Interest
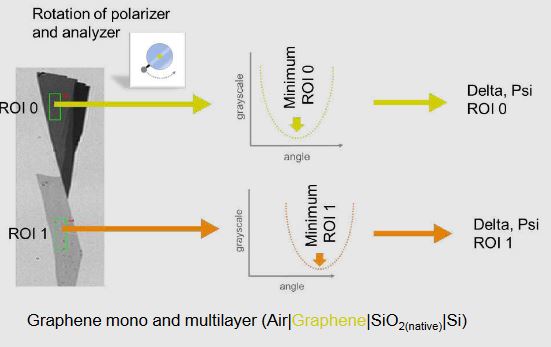
Imaging ellipso- metry offers the option to study portions of the sample by selecting corresponding pixels in the image of the 2D detector.
The intensity changes are recorded only for the pixels, that represent the Region of Interest (ROI). With this method, a much higher lateral resolution is available and similar areas can be measured in parallel.
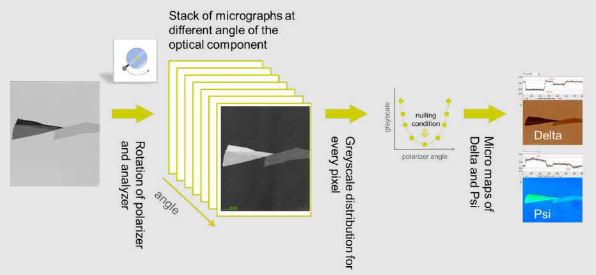
Microscopic Mapping
Microscopic mapping offers the highest lateral resolution in the field of ellipsometry. (down to 1 μm). each pixel works as a single detector.
Psi maps of a MoS2 monolayer at different wavelengths near the direct bandgap
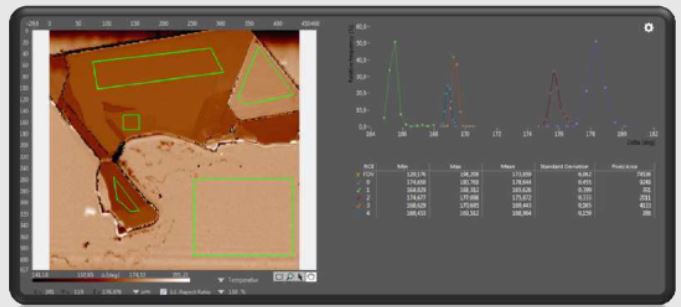
Histograms represen ng different regions of interest of the sample of Delta map at 520 nm of FePS3 flake. Data from maps have a higher sta s cal relevance than single measurements.
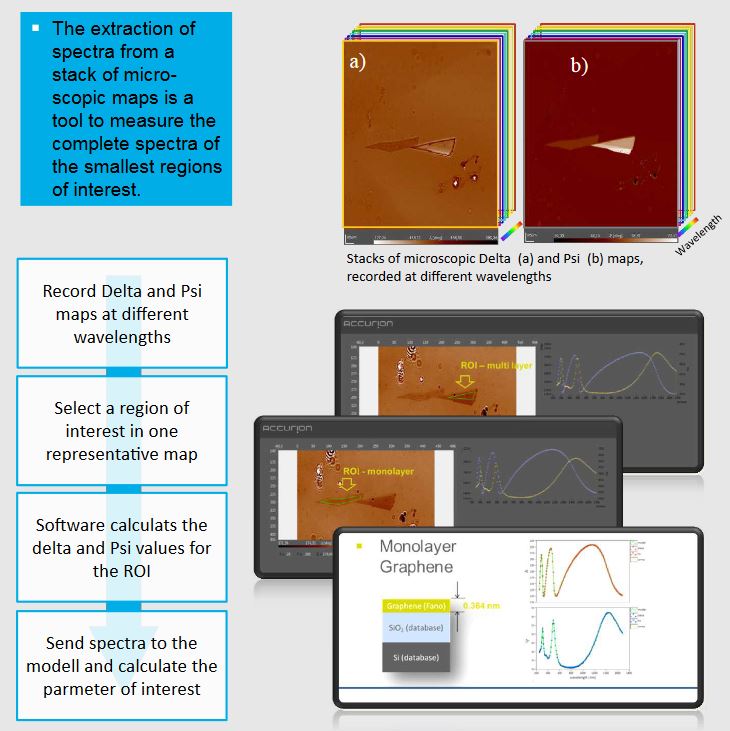
Extracting Wavelength Spectra
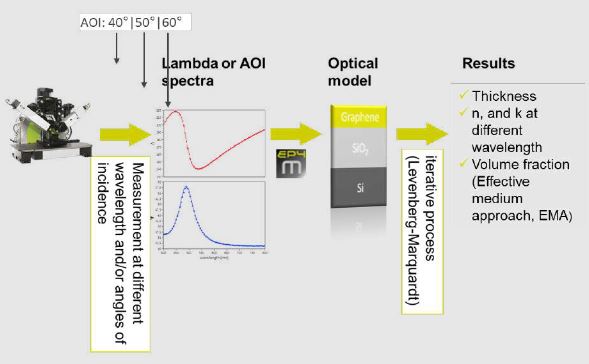
Optical Modeling
Calculation of opti- cal- and metrologi- cal parameters for ultrathin films. Effective medium approach (EMA) also offers information about chemical composition.
The Drude equation connects the ellipsometric angles Delta and Psi with the Total reflection coefficient of the Fresnel equation and on this track with physical parameters like the complex refractive index and the layer thickness. By using different wavelengths the dispersion function of the layers and/or of the substrate is available. The number of fit parameters is related to the number of measured parameters. To increase the number of parameters, angle of incidence, and wavelength spectra can be measured.
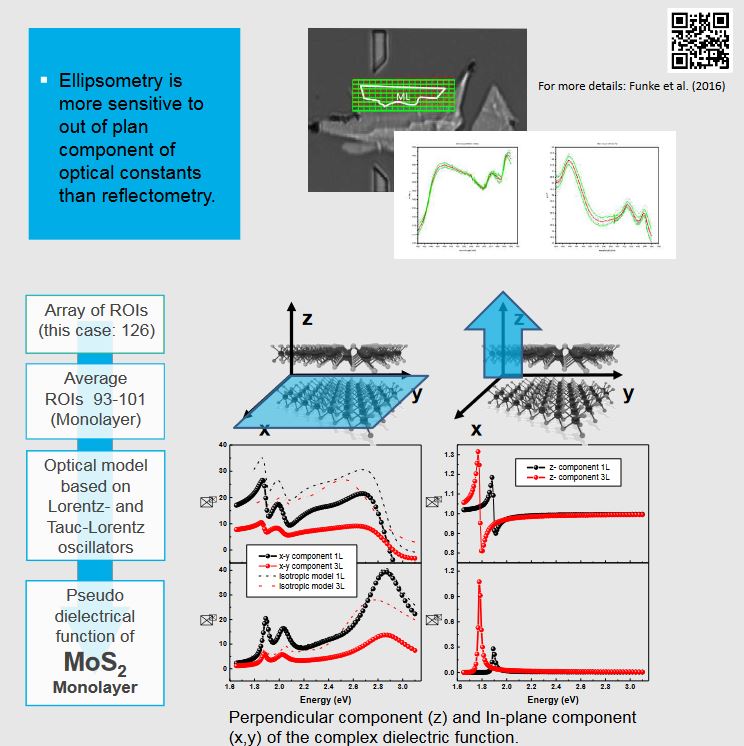
Optical Properties
Knife Edge Illumination
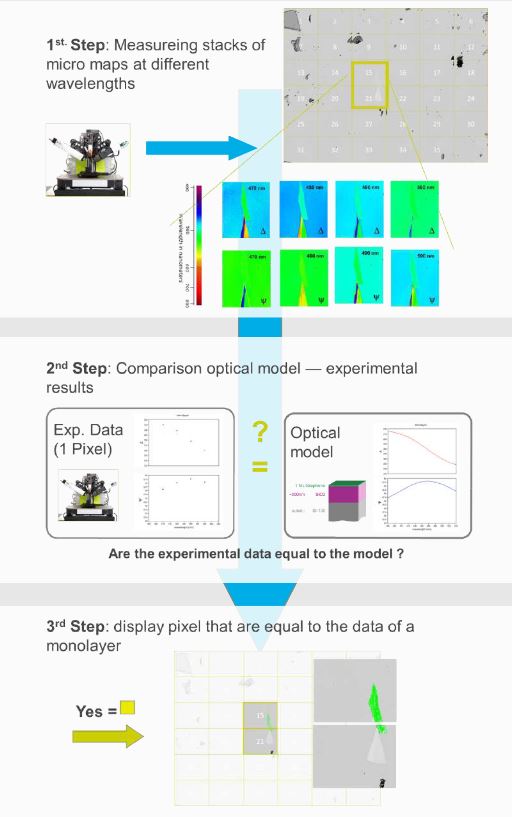
Automatic Flake Search
Calculation of opti- cal- and metrologi- cal parameters for ultrathin films. Effective medium approach offers chemical composition.
Localiza of sample areas with required proper For example, monolayers were iden d by comparing the measured Delta and Psi values with the data from the op cal model. This approach is useful to iden fy monolayers but other proper could also be probed. A er iden an interes ng sample, the tool can be used to search for the same experimental data elsewhere on the sample. This concept has been proven with hex-BN.
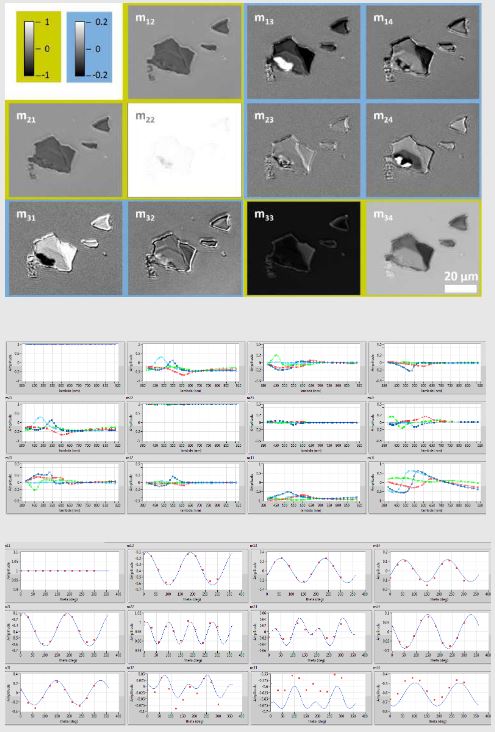
Microscopic Müller Matrix
Müller Matrix Ellipsometry is the method of choice for anisotropic samples. First microscopic Müller Matrix Ellipsometry.
Example: micro- structured flakes of black phosphorus (anisotropic) on silicon substrate.
• Application type: anisotropic thin-film layer.
• Overall focused Mueller- matrix images with microscopic lateral resolution.
• Identification of isotropic and anisotropic regions. • Determination of anisotropic refractive indices and orientation of opitical axis.
Mueller-matrix map at λ=501 nm (a), λ-spectra (b), Theta spectra recorded at different rotational angles of the sample) (c) of anisotropic 2D-material (black phosphorus)